
An R 2 of 1 means the dependent variable can be. An R 2 of 0 means that the dependent variable cannot be. The coefficient of determination ranges from 0 to 1. It is interpreted as the proportion of the variance in theĭependent variable that is predictable from the independent variable. R 2) is a key output of regression analysis. The coefficient of determination (denoted by The least squares regression line is the only straight line that The regression coefficient (b 1) is theĪverage change in the dependent variable ( y) for aġ-unit change in the independent variable ( x). The regression constant (b 0) is equal to the. The regression line passes through the mean of the x. Values (the ŷ values computed from the regression Observed values (the y values) and predicted The line minimizes the sum of squared differences between. When the regression parameters (b 0 and b 1)Ībove, the regression line has the following properties. Where b 0 is the constant in the regression equation, Without a computer or a graphing calculator, you can solve forī 1 = Σ / Σ In the unlikely event that you find yourself on a desert island X and y values into your program or calculator,Īnd the tool solves for the regression constant (b 0) and for the regression coefficient (b 1). Use a computational tool - a software package (e.g., Excel) or a graphing calculator. Predicted value of the dependent variable. 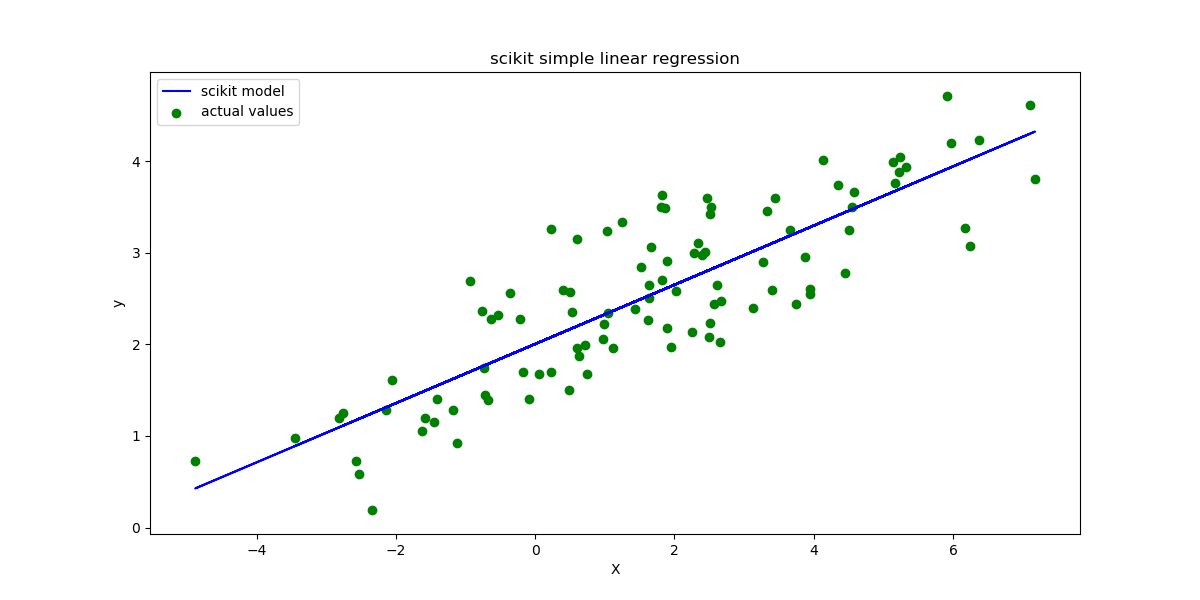
X is the value of the independent variable, and ŷ is the Line is estimated by a sample regression line. Given a random sample of observations, the population regression X is the value of the independent variable, and Y is the Suppose Y is a dependent variable,Īnd X is an independent variable. Least squares regression line or LSRL, thatīivariate data set. Linear regression finds the straight line, called the
The Y values are roughly normally distributedĭotplot will show the shape of the distribution. The Y values are independent, as indicated by a. Satisfied, the variability of the residuals will be relativelyĬonstant across all values of X, which is easily checked in 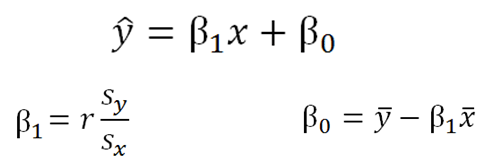 For each value of X, the probability distribution of Y has the. The dependent variable Y has a linear relationship. Simple linear regression is appropriate when the following
For each value of X, the probability distribution of Y has the. The dependent variable Y has a linear relationship. Simple linear regression is appropriate when the following 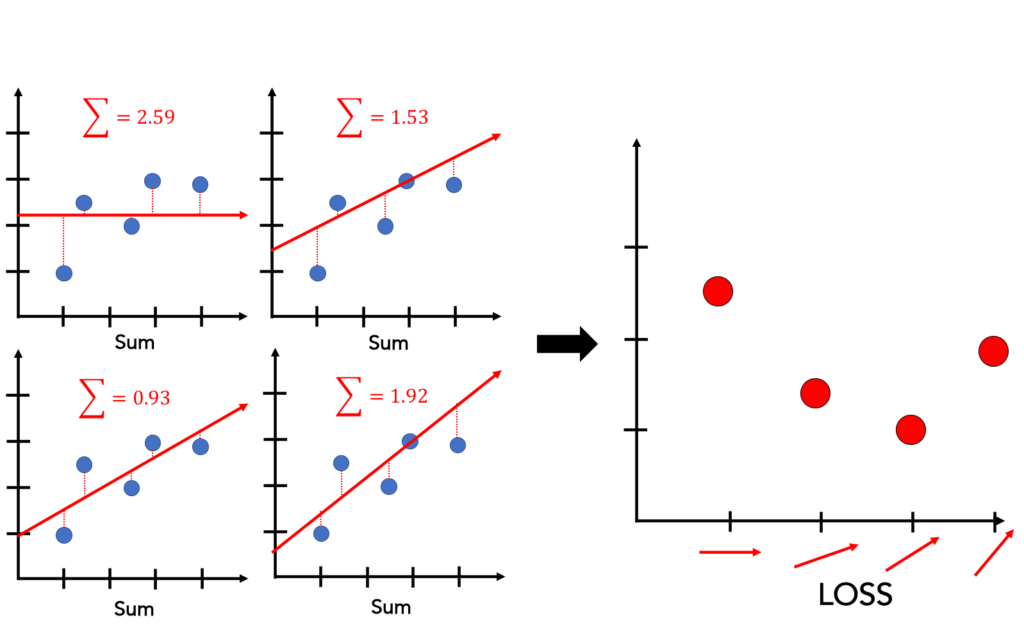
Confidence interval Confidence intervalsĪdvertisement Prerequisites for Regression. Simulation of events Discrete variables. Diff between means Statistical Inference. Experimental design Anticipating Patterns.



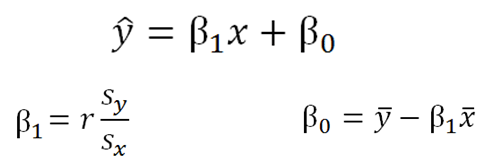



 0 kommentar(er)
0 kommentar(er)
